Well, the Packers just punched their ticket to the Super Bowl…
Up next is the Jets at the Steelers. Game time temp is in the single digits to below zero.
*This is an open thread, OPEN NOT JUST FOOTBALL, discuss whatever you like…we did not put up any serious posts during the games because it would not get the exposure that we want our writers to get.*
Here is some background on the team symbol for the Steelers:
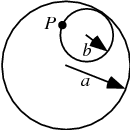
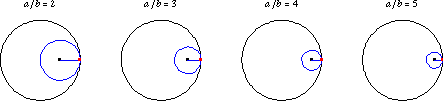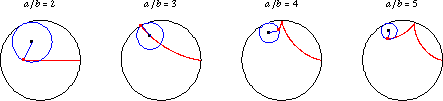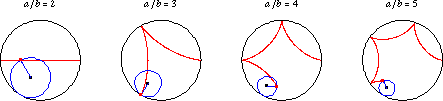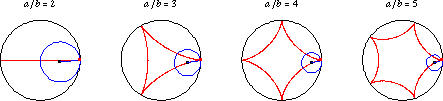
The curve produced by fixed point 
on the circumference of a small circle of radius 
rolling around the inside of a large circle of radius 
. A hypocycloid is therefore a hypotrochoid with 
.
To derive the equations of the hypocycloid, call the angle by which a point on the small circle rotates about its center 
, and the angle from the center of the large circle to that of the small circle 
. Then
 |
(1)
|
so
 |
(2)
|
Call 
. If 
, then the first point is at minimum radius, and the Cartesian parametric equations of the hypocycloid are
 |
 |
 |
(3)
|
 |
 |
 |
(4)
|
 |
 |
 |
(5)
|
 |
 |
 |
(6)
|
If 
instead so the first point is at maximum radius (on the circle), then the equations of the hypocycloid are
 |
 |
 |
(7)
|
 |
 |
 |
(8)
|
The curvature, arc length, and tangential angle of a hypocycloid are given by
 |
 |
 |
(9)
|
 |
 |
 |
(10)
|
 |
 |
 |
(11)
|
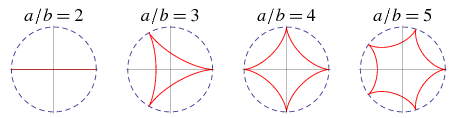
And then:
The Steelmark consists of three four-pointed starlike figures within a circle. The stars in the design approximate a type of geometric figure called an astroid, a particular type of hypocycloid with four cusps.[1][2] A yellow figure is located at the top of the design, orange to the right and blue on the bottom, with the word “Steel” on the left side. The logo appears within a gray ring against a white background.
The logo was incorporated as the emblem of the Pittsburgh Steelers, initially using the same design as the Steelmark, but later modified to include the team’s full name.
Cleveland-based Republic Steel approached the owners of the Pittsburgh Steelers about placing the Steelmark logo on their helmets for the 1962 NFL season, figuring that it would be a perfect product placement for the steel manufacturers.[5] The equipment manager for the team was told to put the logo on the right side of the team’s all-gold helmets. The Steelers went 9–5 that season, their best record to that date. For their first post-season game, in the 1962 Playoff Bowl, the team changed the helmet color from gold to black and it has remained largely unchanged since, with the team the only one in the National Football League to have a logo on only one side of the helmet.[1][6] In 1963, the Steelers petitioned the American Iron and Steel Institute to be allowed to change the word “Steel” in the logo to the full team name, which was approved by the AISI.[1]
In conclusion, if one is a mathematician, then the obvious choice is the Steelers!
Enjoy the games, we will get back to the serious issues on Monday morning.
Tags: NFL Playoffs, Open Thead
